Influence of Discretization in Dynamically Embedded Model Predictive Control

Access the paper here . Accepted to IFAC World Congress 2023

As is known, Model Predictive Control is a popular control scheme for many complex systems. However, implementing it to continuous systems, \(\dot x = f(x,u)\) is almost impossible if we choose to solve a Continuous Time Optimal Control Problem (CT-OCP). So, a more practical method is to solve a Discretised Optimal Control Problem (DT-OCP). One of the ways to find the optimal control law is to solve the DT-OCP using a continuous solver. The result, hereafter referred to as Dynamically Embedded MPC (DE-MPC), is a continuous-time MPC scheme that tracks the solution to the OCP with a bounded error, (Nicotra et al., 2019). In this paper, we analyse the effect of discretisation on DE-MPC. Intuitively having more acccurate discretisation (smaller \(t_d\)) would lead to more stable control law, however that is not true.

Introduction

The DE-MPC scheme is when for a continuous time system, \(\dot x = f(x,u)\), we solve the discretised OCP, (cite) Eq. 8, using a continuous solver, \(\dot z = \mathcal{T}(z,x)\). The optimal control is based on the idea that the solution of the optimal control problem can be embedded in the internal states of a dynamic control law running in parallel to the system.

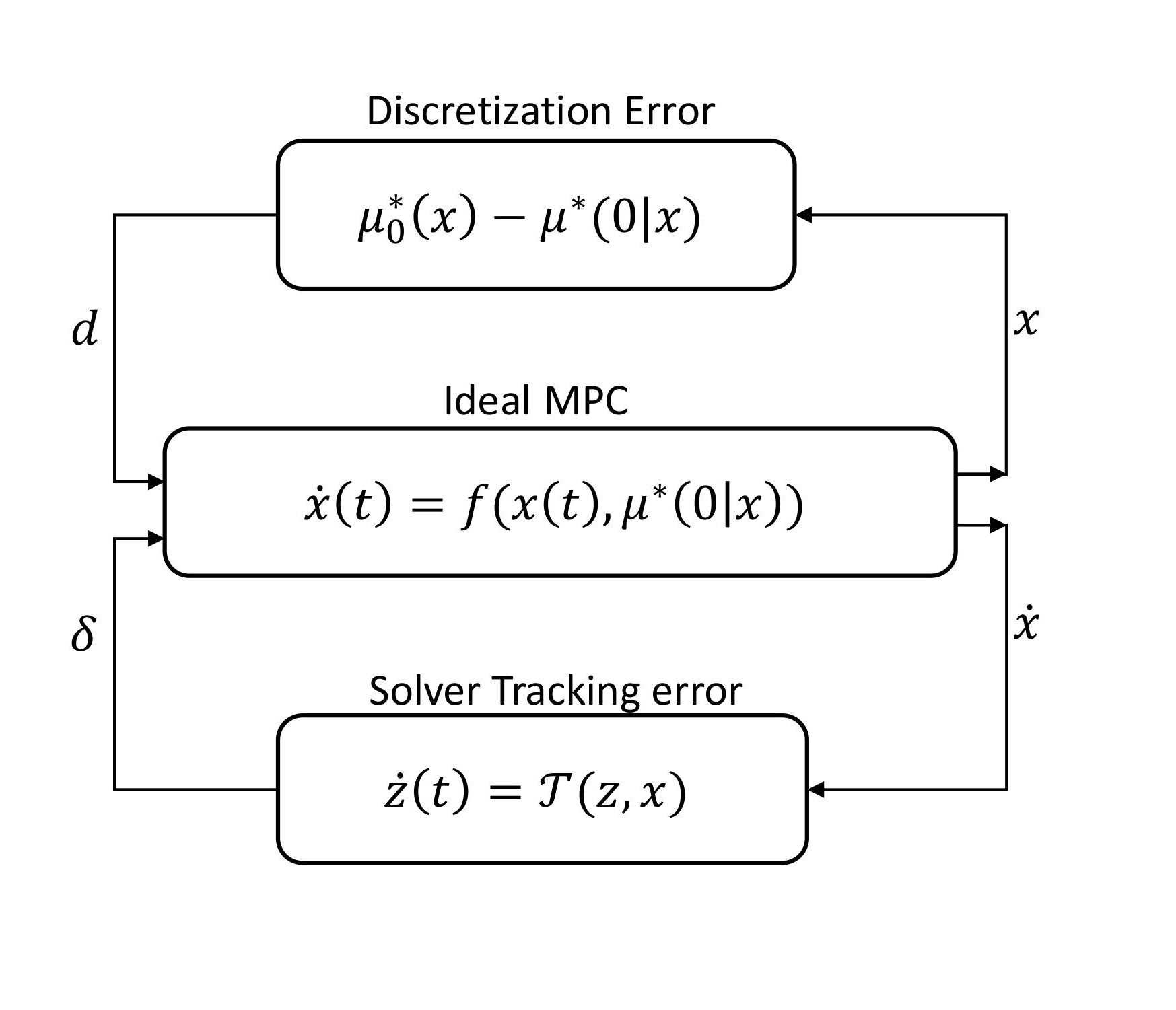
For a fixed prediction horizon \(T\), intuitively, it would make sense that having a smaller discretisation time step \(t_d\), would reduce the discretisation error, making the control law more accurate, however, this does not hold true. While decreasing \(t_d\), the error between the continuous-time optimal control policy and its discrete approximation tends to zero. More importantly, the closed-loop response becomes slower as \(t_d\) increases. This behavior is likely due to the fact that the discretisation becomes increasingly unstable as \(t_d\) increases, thereby causing the discretized control to be overdamped compared to the continuous- time solution.

The solver on the other hand, assuming a fixed parameter \(x\), converges faster for an increasing \(t_d\). This can be explained by noting that higher values of \(t_d\) entail lower \(N = T /td\), thereby meaning that the optimization problem has fewer variables and is therefore easier to solve.

The combination then results in higher values of td simultaneously slowing down the dynamics of the closed- loop system and speed up the convergence rate of the solver. This combined effect makes it easier for the DE- MPC to track the solution of the discretized OCP as the discretization step increases.

Experiments and Results

Numerical Experiments that illustrate the interesting behaviour of discretisation time step variation were conducted. On a point mass system, a Linearised Lane change and a Nonlinearised Lane change problem. The Linearised Lane change example is shown below. The details of the linearised lane change are the same as in (Liao-McPherson et al., 2020) but without the dynamic extension, i.e. the control input u are the steering angles and not their derivatives.

Linearised Lane Change

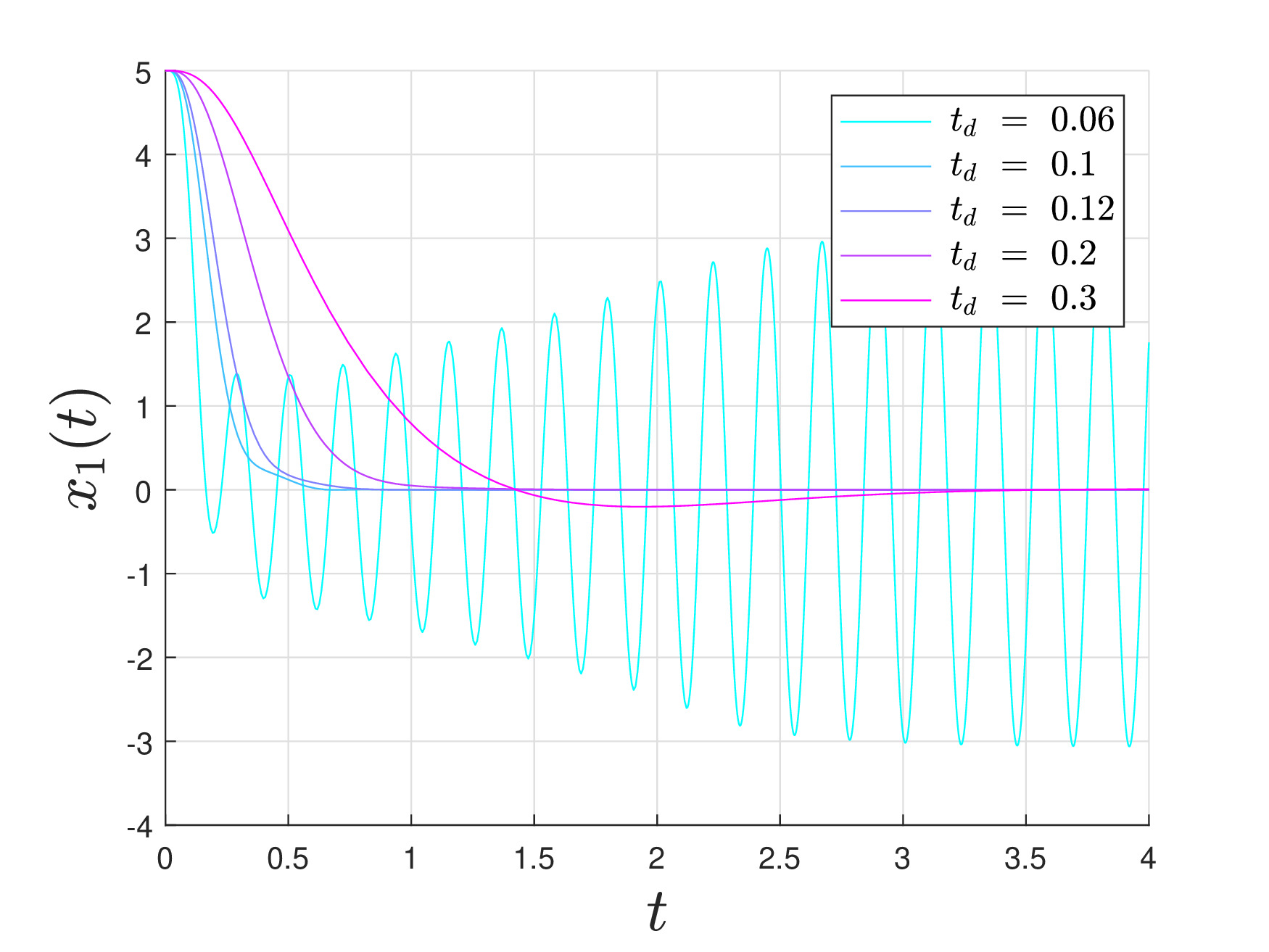
The figured shows position for the Lane change maneuver for a linearized system. Given a fixed solver, the response can be destabilized by selecting an excessively small discretization step.

We verify that, for a fixed flow rate of the solver, lowering td can make the interconnection unstable. To provide more insight on this behavior, (Gautam & Nicotra, 2023) Table 1 reports the eigenvalues of the open-loop matrix Ad and its matrix exponential, with N = T /td. The table shows that decreasing td causes the matrix exponential to have larger eigenvalues which, in turn, causes the optimal control problem to become ill-conditioned. The loss of stability is then explained by the fact that the dynamic solver is too slow compared to the plant, thereby causing the interconnection to become unstable