Compliant Explicit Reference Governor
ERG for contact friendly robotics
Access the preprint here
The Explicit Reference Governor (ERG) is a control scheme that is an optimisation free alternative to controlling complex systems, such as robots (Nicotra & Garone, 2018), (Merckaert et al., 2022) . It uses a reference governor that manipulates the reference, \(r\), creating an auxillary reference such that the system, \(\dot x= f(x,u)\) remains within the safety constraints at all given times. It is worth noting that \(\lim_{t \to \infty} v(t) = r\). To achieve this, the ERG defines the gradient of the auxillary reference \(v\), using a Navigation Field, \(\rho(v,r)\) and a Dynamic Safety Margin, \(\Delta(v,x)\) as shown
\[\dot v = \rho (v,r) \Delta (v, x)\]This reference is then applied to the prestabilised system
\[u = -K_P(x-v)-K_D(\dot x)\]While the ERG is a great scheme that is also computationally inexpensive (Merckaert et al., 2024), it does not differentiate between constraints. We propose a scheme where we can differentiate between hard and soft constraints, giving more flexibility to our robotic systems. We can use this particular feature to be able to make contact friendly robots. We name this scheme Compliant Explicit Reference Governor (CERG).
Introduction
The CERG is a reference management scheme that differentiates between soft and hard constraints for contact friendly robotics. The hard constraints are non-violatable, for example: actuator saturation, torque limitations etc. However, the soft constraints are violatable and allow the robot to interact with the environment. One of the major concerns as the robot interacts with the environment is safety. We deal with this concern using Maximum Energy Limitations, which for simple systems can be converted into Maximum Force Limitations. The CERG algorithm is such that it ensures that soft constraints are only violated if necessary, and the interaction is safe, whereas hard constraints are never violated.
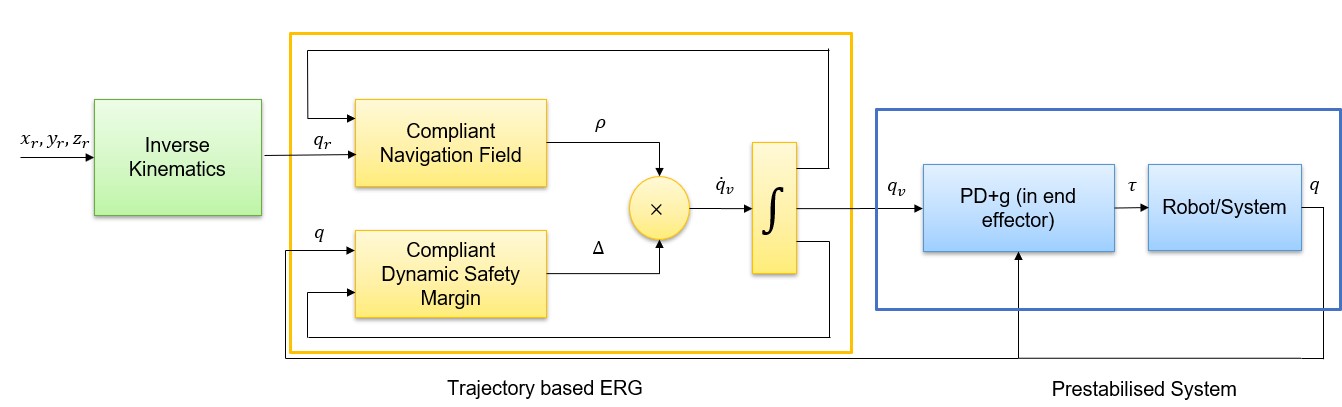
The CERG uses the same basic block diagram as the ERG, however the Compliant Navigation Field and Compliant Dynamic Safety Margin both have two components \(\rho_s(v,r), \rho_h(v,r)\) and \(\Delta_s(v,x), \Delta_h(v,x)\) to deal with soft and hard constraints respecitvely.
In the paper (cite) we prove that the structure of the Compliant Dynamic Safety Margin is such that it ensures that either no constraints are violated, or if necessary, only soft constraints are violated within the energy limitations.
Experiments and Results
Numerical Experiments that validated the premise of the CERG scheme were run on a point mass system, a Two Link Robot Manipulator and on a simulation of the 7-DoF Franka Emika in Drake. All 3 levels of complexities have shown that the CERG performs as expected. The details of the point mass system are discussed in (cite)
Two Link Robot Manipulator
The details of the Two Link Robot can be found in (Lynch & Park, 2017). For the purpose of this example, we choose our prestabilising law to be in end effector frame as shown \(u = -K_P J(q)^\top (f(q) - f(v)) - K_D\dot q + g(q)\) Where \(K_P = 16I_2, K_D = 10I_2\). As seen in the figure below, the \(r\) is beyond the soft constraint. Choosing the control law in end effector space allows the robot end effector to get as close to the constraint as possible, while still remaining under \(E_{/max}\). The discussion on choosing Task Space Controller as opposed to Joint Space Controller is present in the paper. The following figure shows the RR arm under Task Space Control with a very compliant wall
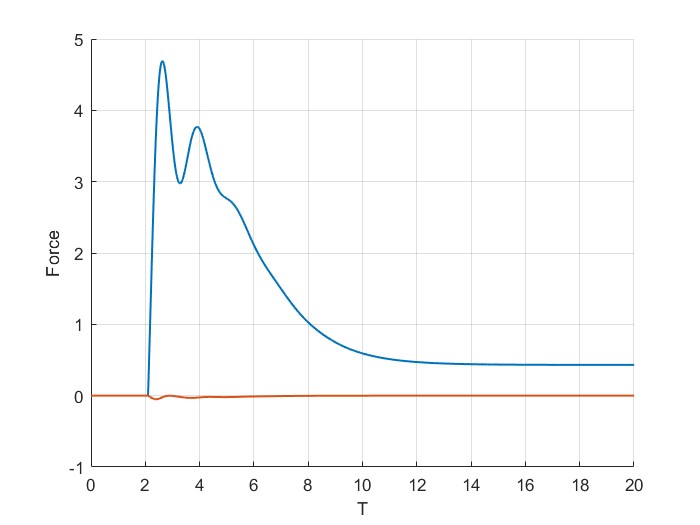
Now to understand the effects of the penetration constant \(\delta_s\), let us set it as \(\delta_s = 0.1F_{\max}/K_P\).
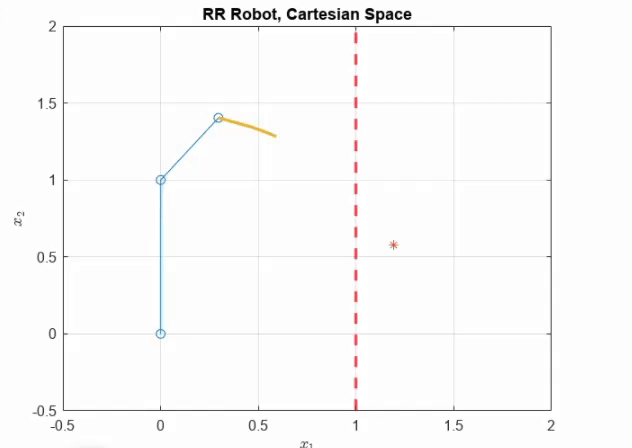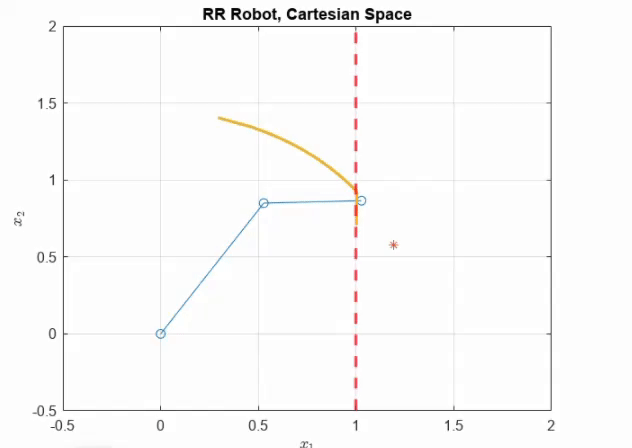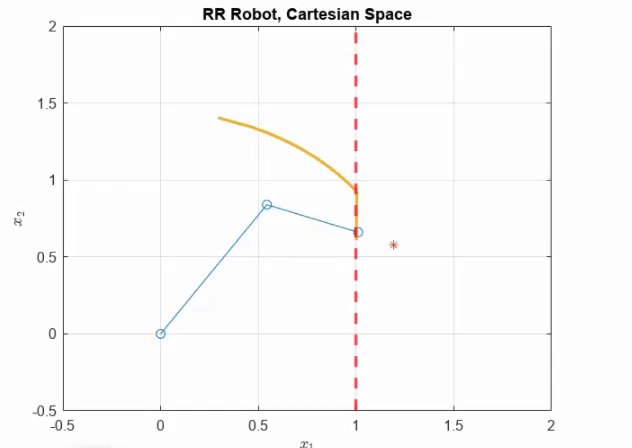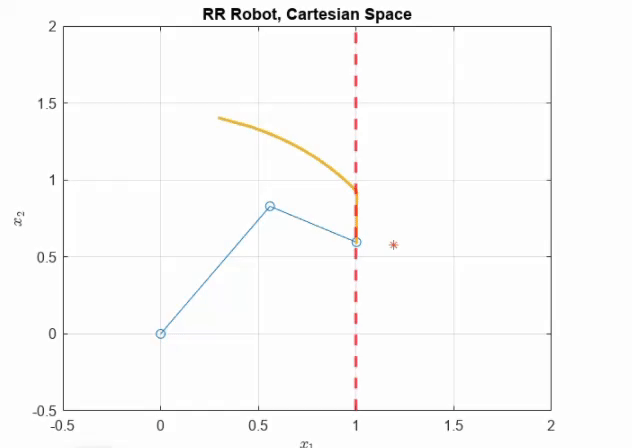
As can be seen, the end effector trajectory of the RR arm slides along the soft wall. Notably, we don’t violate the maximum energy of interaction.
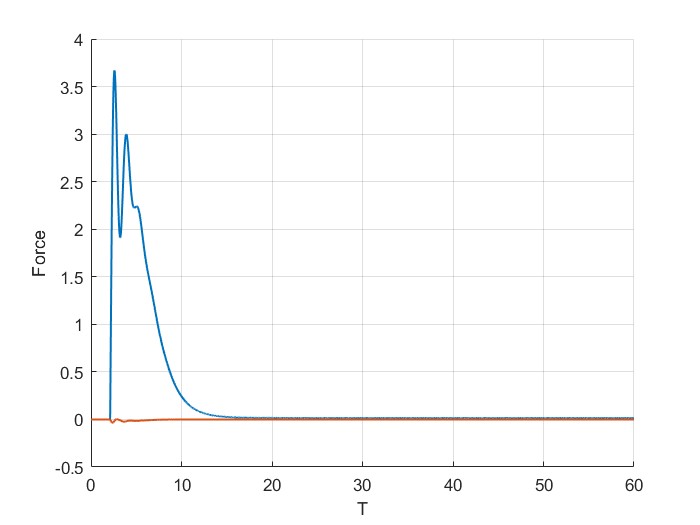
Now, if we set \(\delta_s = 0.9F_{\max}/K_P\). As can be seen, the end effector trajectory enters the soft constraint. The force of pushing is also higher. At steady state we converge to \(F>0\).
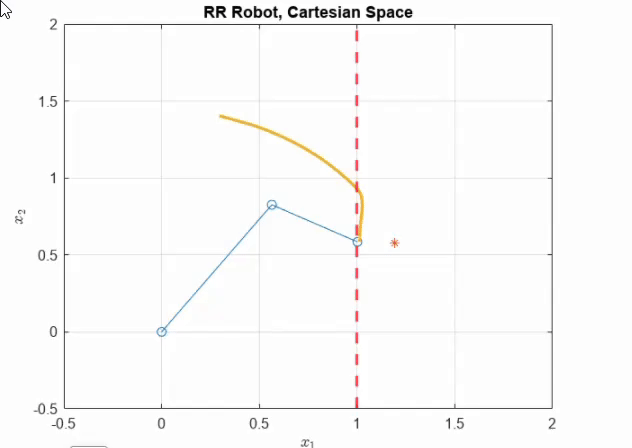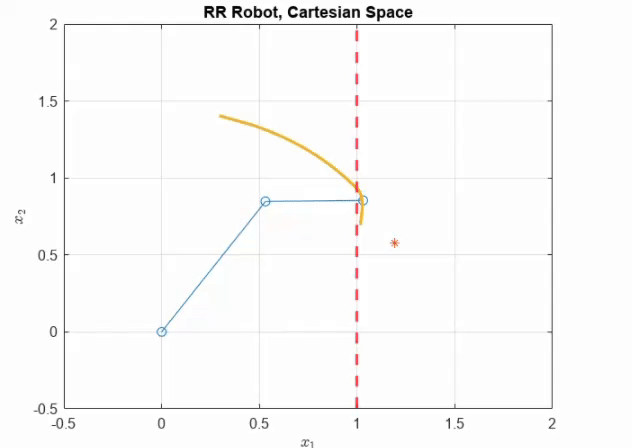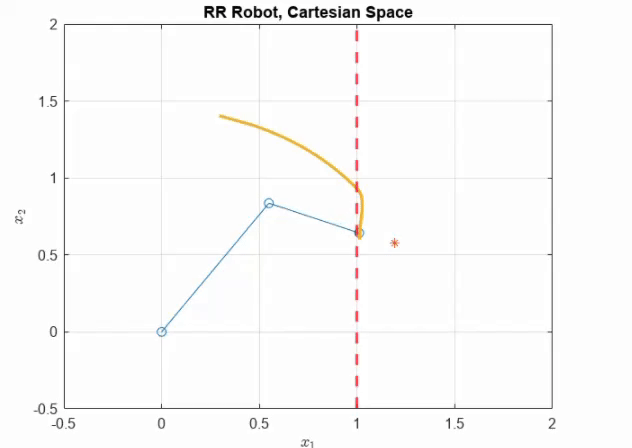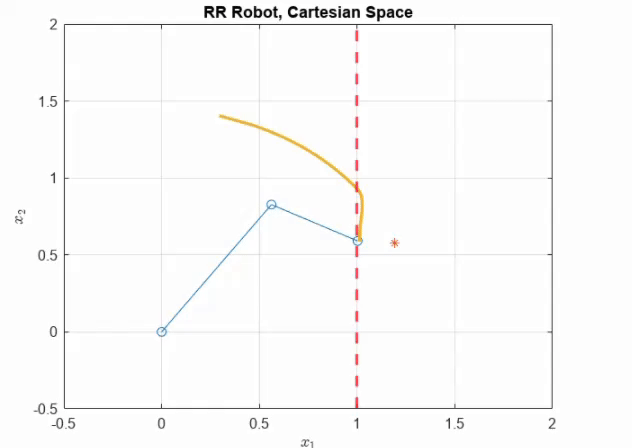
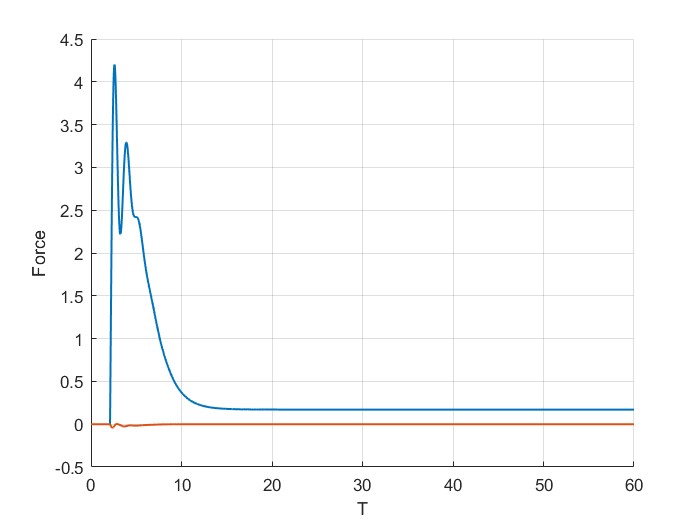
It can be seen from these examples that the penetration constant effects how much we push against our soft constraints. In all cases interestingly, \(F <F_{\max}\), which is set by the maximum energy of interaction \(E_{\max}\), ensuring the safety of interaction.
Drake Simulations of the Franka Emika
Lastly, we demonstrate the CERG on a more realistic simulation on the Franka Emika in Drake simulator. The contact model is chosen to be Compliant Point Contact. The Franka robot is subject to all the actuator, speed and torque limitations as specified here, the reference of the Franka is inside the soft blue wall.

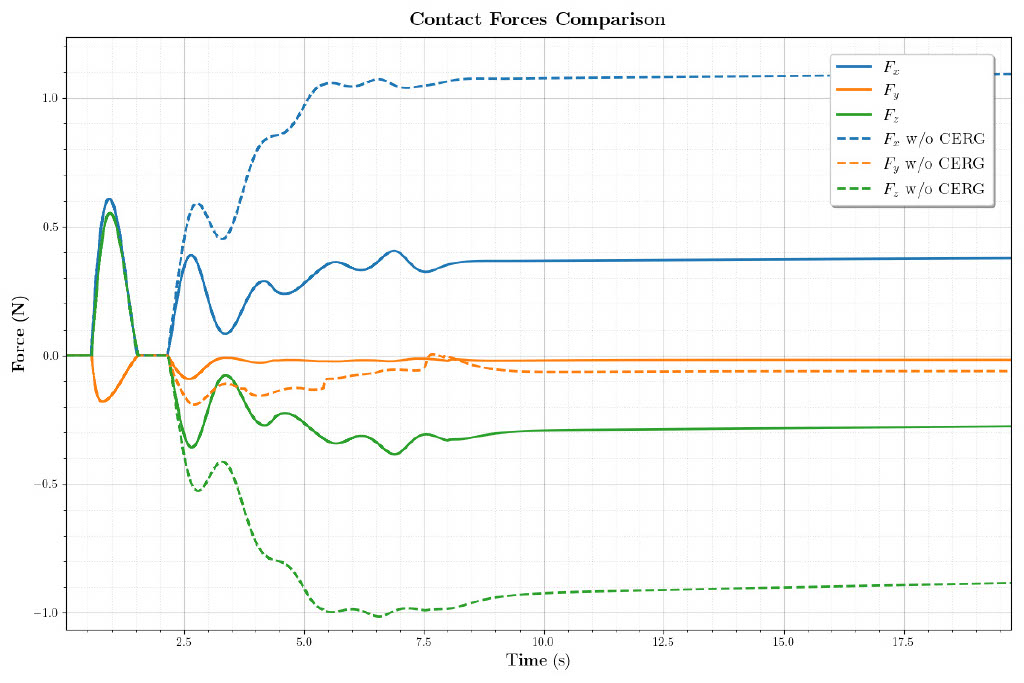
Hardware Experiments on the Franka Emika Panda
We validate the Compliant Explicit Reference Governor (CERG) on real hardware using the Franka Emika Panda robot across two representative manipulation tasks. The objective of these experiments is to assess how CERG enforces hard and soft constraints during contact-rich interaction, modulates the allowable reference motion under different energy bounds, and reduces impact forces during contact transitions.
To contextualize CERG’s performance, we compare it against two baselines:
- Explicit Reference Governor (ERG)
- Finely tuned Cartesian Impedance Controller
The experiments are organized into two subsections below, each describing a task and showing video comparisons between CERG, ERG, and impedance control.
1. Wiping Task
In this task, the robot performs wiping motions over a flat surface. We vary the desired interaction energy bound \((E_{\max}\)) and assess whether each controller can complete the task while respecting the imposed constraints.
CERG adapts the reference trajectory online to satisfy the energy bound \((E_{\max}\)) as well as the hard constraints of joint and velocity limits.
CERG Results
Even when put in different initial conditions far away from the whiteboard,CERG is able to complete the task without difficulty.
For comparison with the Cartesian impedance controller, we consider multiple initial conditions. When tuned to complete the task “perfectly” from a nominal start pose, the impedance controller often drives the robot into joint velocity limit violations or aggressive transients when the initial configuration is perturbed. CERG, in contrast, remains robust across these different initial conditions while still completing the wiping task.
Baseline Controllers: ERG and Impedance
In contrast, the baseline ERG cannot consistently enforce \((E_{\max}\)): for tighter energy limits it either stalls or generates larger contact transients that violate the intended energy budget.
2. Jenga Tower Pushing and Perturbation
In this experiment, the robot interacts with a Jenga tower through controlled lateral pushes and small perturbations. The goal is to inject just enough energy to explore the tower configuration without causing collapse.
CERG maintains a low-energy interaction regime by regulating the reference motion according to the chosen \((E_{\max}\)), preventing large impulsive forces while still allowing meaningful manipulation of the tower. The ERG and impedance baselines, by contrast, frequently produce higher-impact contacts that deform or topple the tower, especially when tuned aggressively for task completion.
CERG Results
Baseline Controllers: ERG and Impedance
Due to the nature of the task, the task is bvery sensitive
References
2024
- Real-time constraint-based planning and control of robotic manipulators for safe human–robot collaborationRobotics and Computer-Integrated Manufacturing, 2024
2022
- Real-time motion control of robotic manipulators for safe human–robot coexistenceRobotics and Computer-Integrated Manufacturing, 2022
2018
- The Explicit Reference Governor: A General Framework for the Closed-Form Control of Constrained Nonlinear SystemsIEEE Control Systems Magazine, 2018
2017
- Modern robotics2017